ラグランジュ力学入門!運動方程式と未定乗数法の導出
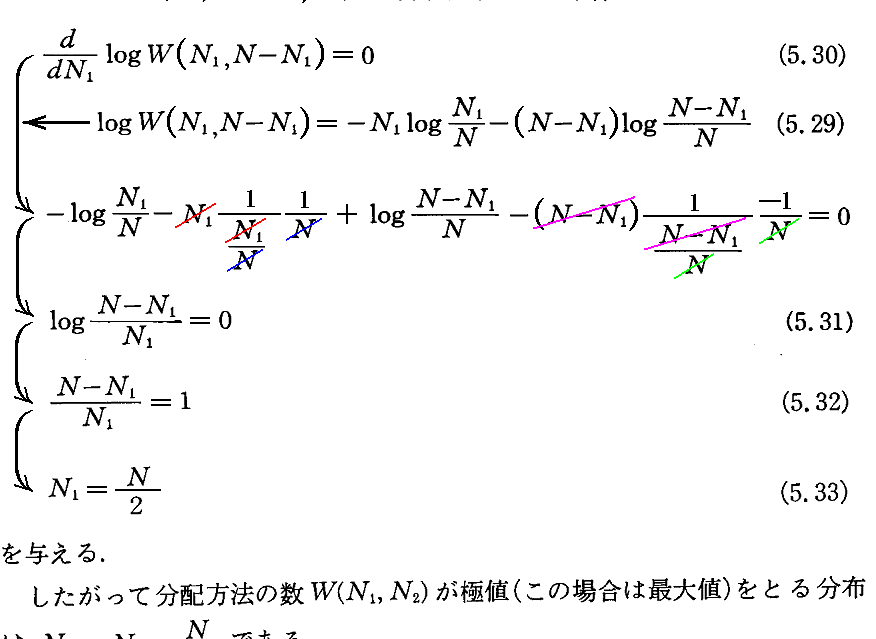
力学の基礎となるラグランジュ力学とは何かを考えます。運動方程式を導出するうえで、ラグランジュの方法が広く用いられています。運動方程式とは、物体の運動を記述する数学的表現であり、力学の中心的な概念です。ラグランジュの方法による運動方程式の導出は、力学の基礎を学ぶうえで不可欠なステップです。この記事では、運動方程式と未定乗数法を用いたラグランジュ力学の導入を行います。力学の初学者でもわかりやすく、基礎を学ぶうえでのステップバイステップのガイドを提供します。
ラグランジュ力学の基礎:運動方程式の導出と未定乗数法の役割
ラグランジュ力学は、クラシカル力学の枠組みにおいて、運動方程式を導出するための強力なツールです。那麼、ラグランジュ力学を入門するために、運動方程式の導出と未定乗数法の役割について、詳しく解説していきます。
運動方程式の導出:ラグランジュ形式の導入
運動方程式は、力学系の運動を記述するための基本方程式です。那麼、運動方程式を導出するために、ラグランジュ形式を導入します。ラグランジュ形式とは、力学系のラグランジアンを定義し、運動方程式を導出するための数学的枠組みです。ラグランジアンは、系の運動エネルギーとポテンシャルエネルギーの差として定義されます。
| 式の定義 | 式の意味 |
|---|---|
| L(q, ∂q/∂t) | ラグランジアン |
| T(q, ∂q/∂t) | 運動エネルギー |
| U(q) | ポテンシャルエネルギー |
運動方程式の導出:オイラー=ラグランジュ方程式
ラグランジュ形式を用いて、運動方程式を導出するために、オイラー=ラグランジュ方程式を導入します。オイラー=ラグランジュ方程式は、ラグランジアンに対する変分原理に基づいて導出されます。変分原理とは、系の運動を最小化するための数学的枠組みです。
Laravelで並列テストを導入!テスト時間を短縮して開発効率アップ未定乗数法:ラグランジュの未定乗数
未定乗数法は、運動方程式を解くための数学的ツールです。那麼、ラグランジュ力学において、未定乗数法を適用するために、ラグランジュの未定乗数を導入します。ラグランジュの未定乗数は、運動方程式の解を導出するために使用されます。
運動方程式の解:一般解の導出
運動方程式を解くために、一般解の導出が必要です。那麼、ラグランジュ力学において、運動方程式の一般解を導出するための方法を紹介します。一般解とは、運動方程式の任意の解を導出するための数学的枠組みです。
ラグランジュ力学の応用:力学系の分析
ラグランジュ力学は、力学系の分析において非常に有効です。那麼、ラグランジュ力学を用いて、力学系の分析を行うための方法を紹介します。力学系とは、物体の運動を記述するための数学的モデルです。
よくある質問
ラグランジュ力学の基本的な考え方とは何ですか?
ラグランジュ力学は、運動方程式を導出するための力学的方法です。ラグランジュ関数を定義して、系の運動を記述します。この方法では、力学系の運動をより簡単に記述することができます。特に、剛体の運動や、電磁気学的な系の運動を記述するのに効果的です。運動方程式を導出することで、系の運動を予測やシミュレーションすることができます。
Laravelバージョンをダウンさせる方法運動方程式とは何ですか?
運動方程式とは、力学系の運動を記述するための数学的な式です。Newtonの運動方程式では、力と加速度の関係を記述します。一方、ラグランジュ力学では、ラグランジュ関数を用いて運動方程式を導出します。この方程式を解くことで、系の運動を予測やシミュレーションすることができます。
未定乗数法とは何ですか?
未定乗数法は、運動方程式を解くための数値計算法です。ニュートン法や、Runge-Kutta法などがあります。この方法では、運動方程式を小さい時間刻みに分割し、各刻みでの系の状態を計算します。この方法を繰り返すことで、系の運動をシミュレーションすることができます。
ラグランジュ力学の応用例は何ですか?
ラグランジュ力学は、様々な分野で応用されています。機械工学では、ロボットの運動をシミュレーションするために使用されます。電気工学では、電磁気学的な系の運動をシミュレーションするために使用されます。また、宇宙工学では、宇宙における衛星の運動をシミュレーションするために使用されます。他にも、様々な分野でラグランジュ力学が応用されています。
Laravelログ入門!操作ログの出力と活用法