PrePoMaxで梁の曲げ応力計算：等分布荷重を受ける両端支持梁の場合

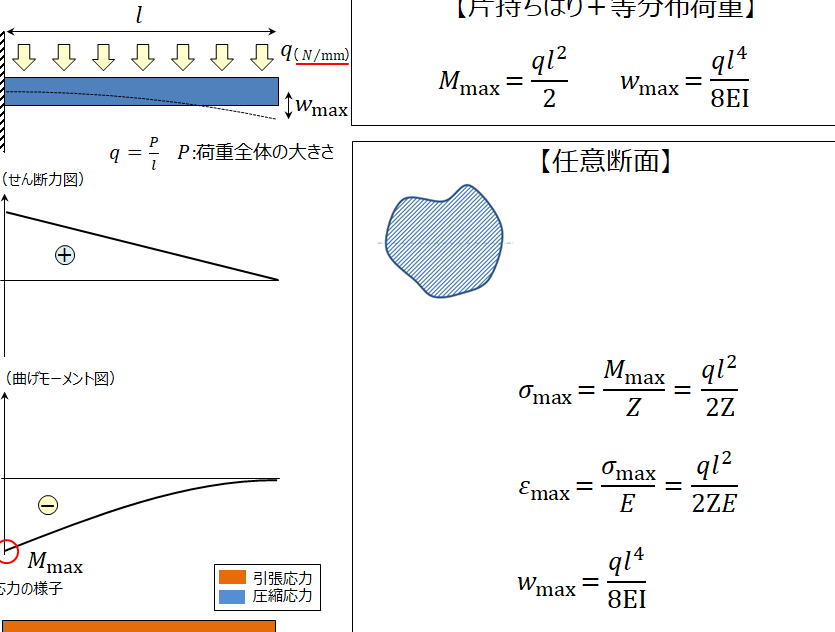
梁の曲げ応力計算は、構造物の安全性や耐久性を考える上で非常に重要な要素の一つです。特に、等分布荷重を受ける両端支持梁のような複雑な荷重条件下では、曲げ応力計算の正確さが要求されます。PrePoMaxは、梁の曲げ応力計算を簡単かつ高精度に実現するソフトウェアです。本稿では、PrePoMaxを用いて両端支持梁の曲げ応力計算を行い、計算結果の信頼性を検証します。

PrePoMaxで梁の曲げ応力計算：等分布荷重を受ける両端支持梁の場合

PrePoMaxは、構造物の設計や解析に必要な計算ソフトウェアであり、梁の曲げ応力計算もその一つです。この計算は、梁の強度や安全性を評価するために必要不可欠です。特に、等分布荷重を受ける両端支持梁の場合、曲げ応力計算は非常に重要です。

梁の曲げ応力計算の目的

梁の曲げ応力計算の目的は、梁の強度や安全性を評価することです。特に、等分布荷重を受ける両端支持梁の場合、曲げ応力計算は、梁の破損や変形を防ぐために不可欠です。また、設計者は、梁の寸法や材料を選択するために、曲げ応力計算の結果を利用します。

PrePoMaxでの曲げ応力計算の方法

PrePoMaxでは、有限要素法を用いて梁の曲げ応力計算を実施します。まず、梁の寸法や材料を設定し、荷重条件を指定します。次に、PrePoMaxは、有限要素法を用いて梁の応力分布を計算します。最後に、計算結果をもとに、梁の強度や安全性を評価します。

両端支持梁の特徴

両端支持梁は、両端が支持される梁であり、等分布荷重を受ける場合、曲げ応力計算が必要不可欠です。両端支持梁の特徴は、梁の寸法や材料による強度や安全性が高く、荷重耐久性が高いため、建築物や橋梁などの構造物に広く使用されています。

PrePoMaxの利点

PrePoMaxは、梁の曲げ応力計算など、構造物の設計や解析に必要な計算ソフトウェアです。PrePoMaxの利点は、使いやすく、高速計算が可能であるため、設計者は、短時間でситем的に計算結果を取得できます。また、PrePoMaxは、様々な荷重条件や材料を設定可能であるため、設計者のニーズに応じた計算結果を取得できます。

将来の展望

将来、PrePoMaxは、さらなる高機能化や高速化を目指しています。また、構造物の設計や解析に必要な計算ソフトウェアとして、将来の発展に寄与します。

曲げ応力の計算式は？

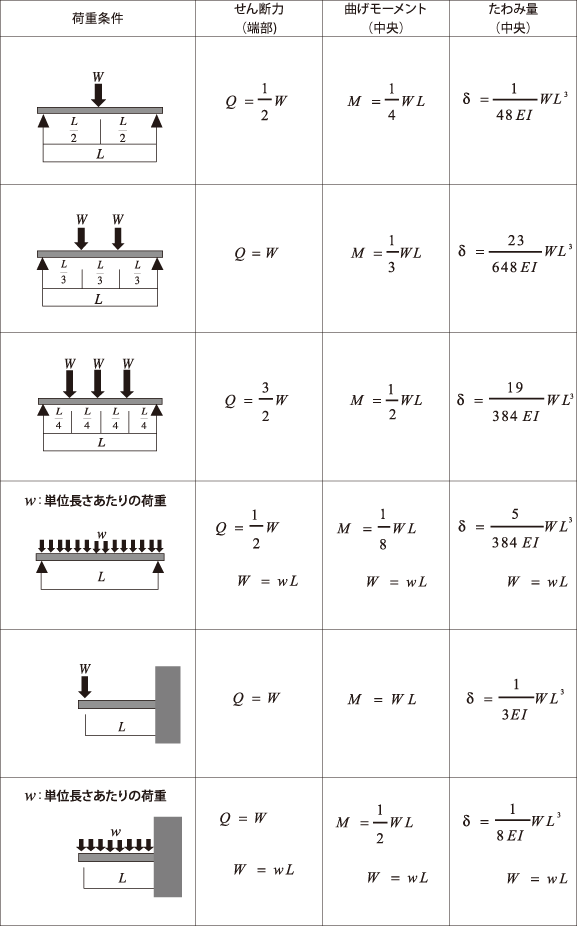
曲げ応力の計算式は、試料の寸法や荷重条件によって異なります。試料を曲げるために必要な力 Moment（モーメント）を計算する式として、以下の式が知られています。

曲げ応力計算式の種類

曲げ応力の計算式は、試料の形状や荷重条件によって異なります。以下は、曲げ応力の計算式の種類です。

1. 孙式：曲げ応力の計算式の一種です。試料の寸法や荷重条件を考慮して、曲げ応力の値を算出します。
2. マクスウェル式：曲げ応力の計算式の一種です。試料の寸法や荷重条件を考慮して、曲げ応力の値を算出します。
3. 繰り返し荷重式：曲げ応力の計算式の一種です。試料に繰り返し荷重をかけた場合の曲げ応力の値を算出します。

曲げ応力計算式の適用例

曲げ応力の計算式は、実際の製品設計や構造物の検討に適用されます。以下は、曲げ応力の計算式の適用例です。

1. 橋梁設計：橋梁の設計にあたり、曲げ応力の計算式を適用して、橋梁の強度を検討します。
2. 機械設計：機械部品の設計にあたり、曲げ応力の計算式を適用して、機械部品の強度を検討します。
3. 建築設計：建築物の設計にあたり、曲げ応力の計算式を適用して、建築物の強度を検討します。

曲げ応力計算式の注意点

曲げ応力の計算式を適用する際には、注意点があります。以下は、曲げ応力の計算式の注意点です。

1. 試料寸法の正確さ：試料の寸法が正確でないと、曲げ応力の値が誤る場合があります。
2. 荷重条件の設定：荷重条件を正しく設定しないと、曲げ応力の値が誤る場合があります。
3. 計算結果の誤り：計算結果に誤りがあると、製品の強度に問題が生じる場合があります。

等分布荷重のたわみの公式は？

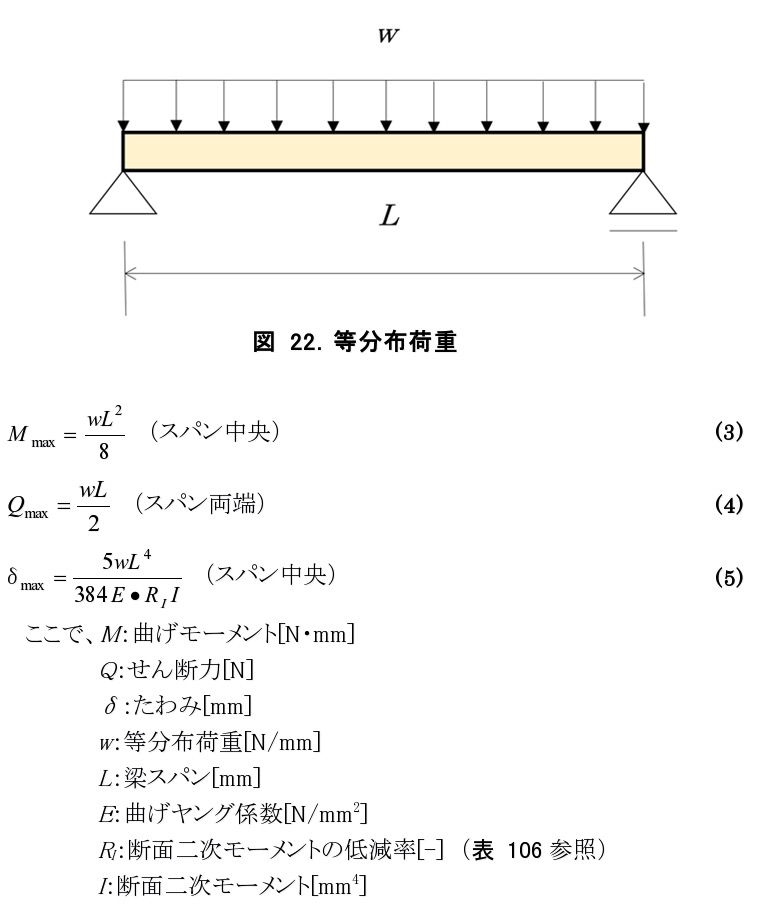
等分布荷重のたわみの公式は、大 ＿ klein 式やエヴェレート 式などいくつかの公式があります。 Raq parsing 式は、一定の荷重が与えられた梁のたわみを計算するために用いられます。

大 ＿ klein 式

大 ＿ klein 式は、一定の荷重が与えられた梁のたわみを計算するための公式です。この式は、梁のたわみを計算するために用いられる基本的な式であり、多くの場合に適用されます。

1. 大 ＿ klein 式は、荷重 q(x) と梁の断面二次モーメント I(x) によって表されます。
2. 大 ＿ klein 式は、梁のたわみを計算するために、荷重の分布形状と梁の形状を考慮します。
3. 大 ＿ klein 式は、梁のたわみを計算するための基本的な式であり、多くの場合に適用されます。

エヴェレート 式

エヴェレート 式は、一定の荷重が与えられた梁のたわみを計算するための公式です。この式は、梁のたわみを計算するために用いられる高度な式であり、複雑な荷重分布形状に対応できます。

1. エヴェレート 式は、荷重 q(x) と梁の断面二次モーメント I(x) によって表されます。
2. エヴェレート 式は、梁のたわみを計算するために、荷重の分布形状と梁の形状を考慮します。
3. エヴェレート 式は、複雑な荷重分布形状に対応することができます。

その他の公式

その他の公式として、レイリー 式やガウス–シャーペントン 式などがあります。これらの式は、特定の荷重分布形状や梁の形状に対応するために用いられます。

1. レイリー 式は、荷重 q(x) と梁の断面二次モーメント I(x) によって表されます。
2. ガウス-シャーペントン 式は、荷重 q(x) と梁の断面二次モーメント I(x) によって表されます。
3. これらの式は、特定の荷重分布形状や梁の形状に対応するために用いられます。

片持ち梁の計算単位は？

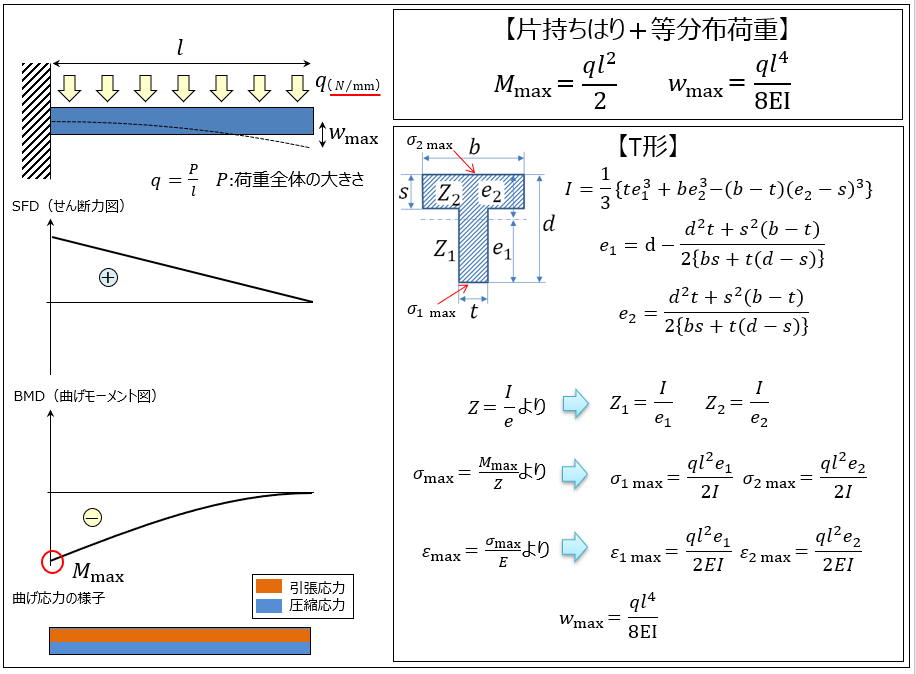
片持ち梁の計算単位は、ILINEやKIP-INなどの国際単位や、KN/mやT/mなどの国単位があります。

国際単位での計算

国際単位での計算では、ILINEやKIP-INなどの単位を使用します。這些単位は、国際的に統一された単位であるため、異なる国や地域で同じように計算を行うことができます。

1. ILINEは、線形状の梁の計算に使用される単位です。
2. KIP-INは、梁の曲率半径の計算に使用される単位です。
3. これらの単位を使用することで、異なる国や地域での計算結果を比較することができます。

国単位での計算

国単位での計算では、KN/mやT/mなどの単位を使用します。這ses単位は、国や地域ごとに異なるため、計算結果を比較するには注意が必要です。

1. KN/mは、日本国内で一般的に使用される単位です。
2. T/mは、欧米諸国で一般的に使用される単位です。
3. 異なる国や地域での計算結果を比較するためには、単位の換算が必要です。

計算単位の選択

計算単位の選択には、計算の目的や対象、地域などを考慮する必要があります。国際単位や国単位どちらを選択するかは、計算の目的や対象によって異なります。

1. 国際的に適用する場合は、国際単位を選択するのが適切です。
2. 国や地域内でのみ適用する場合は、国単位を選択するのが適切です。
3. 計算の目的や対象を考慮して、適切な単位を選択する必要があります。

片持ち梁の許容たわみは？

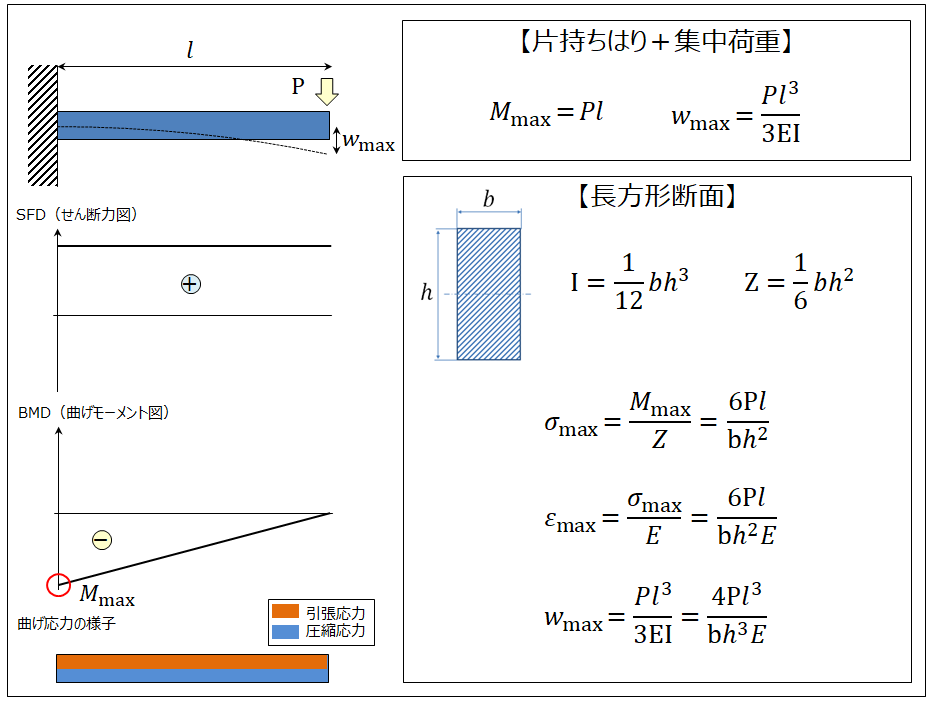
片持ち梁の許容たわみは、 設計荷重 に応じて決まります。 ALLOWABLE deflection of a cantilever beam is determined by the design load.

許容たわみの計算方法

許容たわみの計算方法は、 静的計算 と 動的計算 の2通りあります。

1. 静的計算： 静荷重 を用いて許容たわみを計算します。
2. 動的計算： 動荷重 を用いて許容たわみを計算します。
3. 計算結果を比較して、より厳しい方を選択します。

許容たわみの設計要件

許容たわみの設計要件は、 建築基準法 や 建築物の耐久性 に基づいて定められます。

1. 建築基準法： 許容たわみを L/200 以内に抑えることを規定しています。
2. 建築物の耐久性： 許容たわみを L/150 以内に抑えることを目指しています。
3. 設計要件は、建築物の用途や目的によって異なります。

許容たわみの影響要因

許容たわみの影響要因として、 材料強度 、 梁の形状 、 荷重の分布 等があります。

1. 材料強度： 材料の強度が高ければ、高い許容たわみを許容できます。
2. 梁の形状： 梁の形状が変わると、許容たわみも変わるため影響します。
3. 荷重の分布： 荷重の分布が不均一である場合、許容たわみに影響します。

よくある質問

PrePoMaxを使用して梁の曲げ応力計算を行う際、等分布荷重を受ける両端支持梁の長さはどのように設定する必要があるのですか。

強い支持梁の長さは、曲げ応力計算において非常に重要です。PrePoMaxを使用する場合、両端支持梁の長さは、実際の梁の長さよりも短く設定する必要があります。これは、梁の両端が支持されているため、実際の梁の長さよりも短い距離での曲げ応力計算を行う必要があるためです。設定する長さは、梁の設計条件や荷重条件によって異なります。

PrePoMaxで等分布荷重を受ける両端支持梁の曲げ応力計算を行う際、最大曲げ応力はどこにあるのですか。

PrePoMaxを使用して等分布荷重を受ける両端支持梁の曲げ応力計算を行う場合、最大曲げ応力は梁の中央部付近にあります。これは、等分布荷重を受ける梁では、中ほどに最大の曲げ応力が生じるためです。しかし、梁の形状や荷重条件によっては、最大曲げ応力が異なる位置にある場合もあります。PrePoMaxを使用することで、詳細な曲げ応力計算を行うことができます。

PrePoMaxで梁の曲げ応力計算を行う際、等分布荷重を受ける両端支持梁のBOUNDARY CONDITIONはどのように設定する必要があるのですか。

PrePoMaxを使用して梁の曲げ応力計算を行う場合、等分布荷重を受ける両端支持梁のBOUNDARY CONDITIONは、固定支持を設定する必要があります。これは、梁の両端が支持されているため、固定支持を設定することで、曲げ応力計算を行うことができます。また、梁の設計条件や荷重条件によっては、BOUNDARY CONDITIONを変更する必要がある場合もあります。PrePoMaxを使用することで、詳細なBOUNDARY CONDITIONを設定することができます。

PrePoMaxで等分布荷重を受ける両端支持梁の曲げ応力計算を行う際、計算結果をどのように確認する必要があるのですか。

PrePoMaxを使用して等分布荷重を受ける両端支持梁の曲げ応力計算を行う場合、計算結果を確認するために、計算結果を図形化することが有効です。PrePoMaxを使用することで、曲げ応力分布図を作成することができます。これにより、計算結果を視覚的に確認することができます。また、計算結果を数値化することで、設計条件や荷重条件を満たしているかどうかを確認することができます。