Pythonで一般ガウス状態空間モデルを実装!
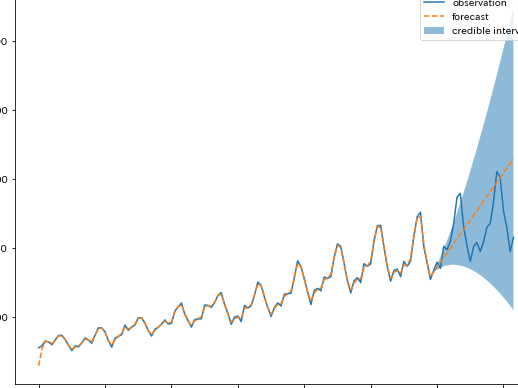
ガウス状態空間モデルは、時系列データの分析に広く用いられている重要なモデルの一つです。このモデルでは、観測値がガウス分布に従うことを仮定し、状態変数を推定することで、将来の観測値を予測することができます。特に、Pythonのpopularな機械学習ライブラリScikit-learnでは、ガウス状態空間モデルの実装が提供されていません。しかし、本稿では、Pythonで一般ガウス状態空間モデルを実装する方法を紹介します。具体的には、Pythonの数値計算ライブラリNumPyやSciPyを用いて、ガウス状態空間モデルのアルゴリズムを実装し、時系列データの分析に役立つツールを開発します。
Pythonで一般ガウス状態空間モデルを実装!
Pythonでは、 NumPy や SciPy などのライブラリを使用することで、一般ガウス状態空間モデルを実装することができます。一般ガウス状態空間モデルとは、状態空間の各要素がガウス分布に従うという仮定のもとに、状態空間モデルの推定を行う手法です。この手法により、状態空間モデルのパラメータ推定や予測、フィルタリングなどが可能になります。
一般ガウス状態空間モデルの基本
一般ガウス状態空間モデルは、状態空間モデルの一種で、状態空間の各要素がガウス分布に従うことを仮定します。このモデルでは、状態空間の各要素が一緒にガウス分布に従うと仮定することで、状態空間モデルの推定を行うことができます。
Pythonで学ぶ制御工学:P・PI・PID制御入門| パラメータ | 説明 |
|---|---|
| 状態空間の次元数 | 状態空間の次元数を指定します。 |
| 観測行列 | 観測行列を指定します。 |
Pythonでの実装手順
Pythonでの一般ガウス状態空間モデルの実装手順は、以下の通りです。 1. NumPy や SciPy などのライブラリをインポートします。 2.状態空間モデルのパラメータを指定します。 3. ガウス分布に基づいて状態空間モデルの推定を行います。 4. 推定結果を用いて予測やフィルタリングを行います。
状態空間モデルのパラメータ推定
状態空間モデルのパラメータ推定では、最尤推定やベイズ推定などの手法を使用します。これらの手法により、状態空間モデルのパラメータを推定することができます。
| 手法 | 説明 |
|---|---|
| 最尤推定 | 最尤推定は、観測データに基づいて状態空間モデルのパラメータを推定します。 |
| ベイズ推定 | ベイズ推定は、観測データに基づいて状態空間モデルのパラメータを推定します。 |
予測とフィルタリング
一般ガウス状態空間モデルの予測とフィルタリングでは、推定されたパラメータを用いて将来の状態や観測値を予測します。フィルタリングでは、現在の状態を用いて将来の状態を予測します。
NumPy や SciPy の利用
NumPy や SciPy などのライブラリは、一般ガウス状態空間モデルの実装に必要な数学的操作を提供します。これらのライブラリを使用することで、状態空間モデルの推定や予測、フィルタリングなどを効率的に行うことができます。
Pythonでデータ型判定:数字?文字列?状態空間モデルとは?
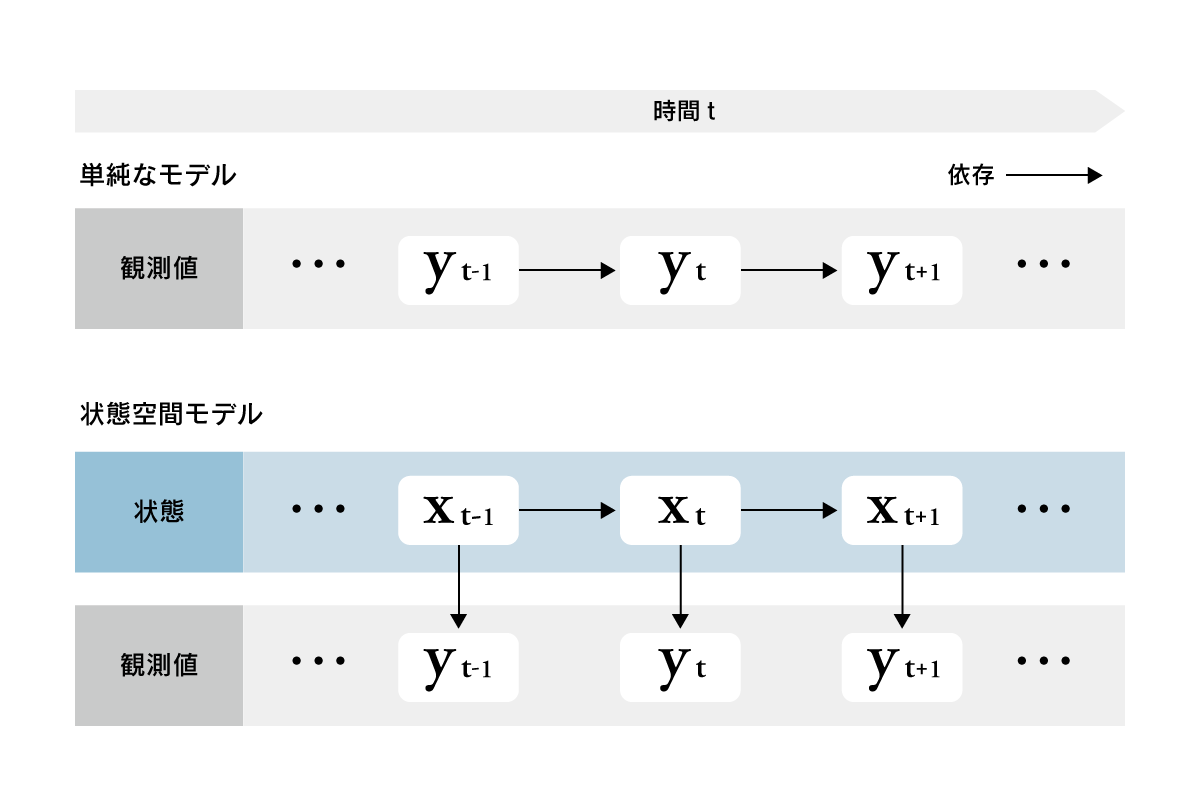
状態空間モデルとは、システムや現象を数学的にモデル化するための手法の一つですそれは、状態変数の時間的変化を表現するために、離散的な状態空間を導入しますこのモデルでは、状態変数の時間的変化をマルコフ性の仮説に基づいてモデル化し、未来の状態を予測することができます
状態空間モデルの特徴
状態空間モデルには、以下のような特徴があります
- マルコフ性: 状態変数の時間的変化は、現在の状態しか関与しないという仮説に基づいてモデル化します
- 離散的な状態空間: 状態変数を離散的な値に離散化し、状態空間を導入します
- モデルの線形性: モデルは線形にすることができ、計算が容易になります
状態空間モデルの適用分野
状態空間モデルは、以下のような分野で広く適用されています
Pythonでガチャシステム実装:BOXガチャ編- 制御工学: システムの制御や最適制御のために、状態空間モデルを用いてシステムをモデル化します
- 信号処理: 信号処理のためのフィルターや推定器の設計に状態空間モデルを用います
- 金融工学: 金融市場の予測やポートフォリオの最適化のために、状態空間モデルを用います
状態空間モデルの種類
状態空間モデルには、以下のような種類があります
- 線形状態空間モデル: 状態変数が線形的に変化するモデルです
- 非線形状態空間モデル: 状態変数が非線形的に変化するモデルです
- ハイブリッド状態空間モデル: 状態変数が離散的かつ連続的に変化するモデルです
状態空間モデルとARIMAモデルの違いは何ですか?
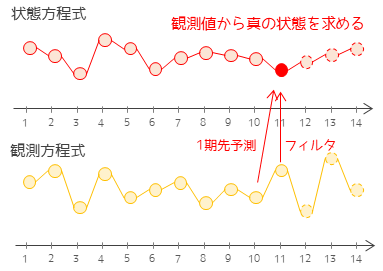
状態空間モデル(State Space Model)とARIMAモデル(AutoRegressive Integrated Moving Average Model)は、時系列分析において広く用いられるモデルですが、異なる目的と特徴を持っています。
モデル構造の違い
状態空間モデルの構造は、観測値と状態ベクトルの関係を明確に捉えることができます。具体的には、状態方程式と観測方程式の2つから構成されます。一方、ARIMAモデルの構造は、過去の観測値に基づいて現在の観測値を予測することを目的としています。ARIMAモデルの構造は、自己回帰項、積分項、移動平均項の3つから構成されます。
Python波動シミュレーション:遊びながら学ぼう!- 状態空間モデルの構造は、物理的なシステムの動作原理に基づいており、システムの状態を明確に捉えることができます。
- ARIMAモデルの構造は、統計的な関係に基づいており、過去の観測値の相互関係を捉えることができます。
- 状態空間モデルのパラメーターの推定には、EMアルゴリズムやParticle Filterなどが用いられます。
適用範囲の違い
状態空間モデルは、システムの状態を明確に捉えることができるため、物理的なシステムの分析や予測に向いています。一方、ARIMAモデルは、時系列データの分析や予測に向いています。
- 状態空間モデルは、気象観測や機械制御などの物理的なシステムの分析に向いています。
- ARIMAモデルは、株価予測や売り上げ予測などの経済的な時系列データの分析に向いています。
- 状態空間モデルは、 mås 高次元の状態を捉えることができます。
推定の違い
状態空間モデルのパラメーターの推定には、最大尤度推定やベイズ推定などが用いられます。一方、ARIMAモデルのパラメーターの推定には、最小二乗推定やべき分布推定などが用いられます。
- 状態空間モデルのパラメーターの推定には、EMアルゴリズムやParticle Filterなどが用いられます。
- ARIMAモデルのパラメーターの推定には、 INFORMATION CriterionやCross Validationなどが用いられます。
- 状態空間モデルのパラメーターの推定には、高次元の状態を捉えることができます。
よくある質問
Q1: Pythonで一般ガウス状態空間モデルを実装する必要性はどこにあるのですか:
ガウス状態空間モデルは、時系列データを分析するための有力な手法として、機械学習や信号処理の分野で広く用いられています。特に、Pythonを用いて実装することで、フレキシブルなモデル構築や高速な計算が実現できます。そのため、 Pythonで一般ガウス状態空間モデルを実装する必要性は、データ分析や予測モデルの構築において非常に高く、実践的なアプローチをならすための基礎として位置づけられます。
Q2: 一般ガウス状態空間モデルの理論的背景は何か:
ガウス状態空間モデルは、線形系やガウス過程という数学的理論に基づいています。これらの理論を理解することで、モデル構築やパラメータ推定の過程をより適切に理解し、効果的なモデリングを実現できます。また、ベイズ統計や情報幾何の理論とも深い関連があり、統計的モデリングの視点からも捉えることができます。
Q3: Pythonで一般ガウス状態空間モデルを実装するための主要なライブラリは何か:
Pythonで一般ガウス状態空間モデルを実装するためには、SciPyやStatsmodelsなどの数値計算や統計分析のライブラリを用いることができます。また、Pykalmanやfilterpyなどの専門的なライブラリもあり、ガウス状態空間モデルの実装を支援します。これらのライブラリを適切に組み合わせることで、高品質なモデルを実現できます。
Q4: 一般ガウス状態空間モデルの実際的な応用例は何か:
ガウス状態空間モデルは、経済指標の予測や気象予報のための時系列データの分析、信号処理のためのノイズ除去やフィルタリング、ロボット工学におけるステート推定など、多くの分野において実際的に適用されています。また、 IoT デバイスのためのセンサーデータの分析やヘルスケアにおける生体信号の分析も含まれています。そのため、 Pythonで一般ガウス状態空間モデルを実装することで、実践的な問題を解決するための強力なツールを手に入れることができます。