【Python】変分問題をわかりやすく解説!計算例も紹介

Pythonにおける数理最適化の一分野である変分問題。それはいわゆる「無限ccbapeの最適化問題」と呼ばれ、解析力や計算性能に影響を与える重要な技術です。特に、機械学習やデータサイエンスの分野で多くの問題に適用され、重要性が増しています。しかし、変分問題自体が難しく、初心者にとって取り組むのが困難です。この記事では、変分問題の基本的な理論や計算方法をわかりやすく解説し、具体的な計算例を交えて、みんなにとってわかりやすいcontentsを目指しています。
【Python】変分問題の基本概念を理解しよう!
変分問題は、数学や物理学で広く用いられる重要な概念です。Pythonを用いて変分問題を解くことで、より深く理解することができます。この記事では、変分問題の基本概念と、Pythonを用いての計算例を紹介します。
【変分問題の定義】
変分問題とは、関数の最小化や最大化を目指す問題です。具体的には、与えられた関数を最小化するために、関数の引数を変化させることで、最適な値を求める問題です。Pythonを用いて変分問題を解くことで、複雑な計算を簡単に行うことができます。
| 問題の名称 | 問題の定義 |
|---|---|
| 最小化問題 | 関数の最小化 |
| 最大化問題 | 関数の最大化 |
【変分問題の種類】
変分問題には、幾つかの種類があります。最も基本的なものは、関数の最小化問題と関数の最大化問題です。また、制約付き変分問題や動的変分問題など、より複雑な問題もあります。
【Python】文字列と数値(asciiコード)の変換方法まとめ【Pythonを用いた変分問題の計算】
Pythonを用いて変分問題を計算することで、複雑な計算を簡単に行うことができます。SciPyというライブラリを用いることで、変分問題を解くことができます。
【SciPyを用いた変分問題の例】
SciPyを用いて、最小化問題を解く例を紹介します。例えば、次のような関数を最小化する問題を考えます。 f(x) = x^2 + 2y^2 この問題をSciPyを用いて解くと、最適な値を求めることができます。
【変分問題の応用】
変分問題は、機械学習や最適化問題など、多くの分野で応用されています。具体的には、機械学習のパラメーターの最適化やコスト関数の最小化など、変分問題を用いることで、より良い成果を導くことができます。
よくある質問
Q1: 変分問題って何ですか?
変分問題は、最適化問題の一種で、一定の条件下での最小値や最大値を探索することを目的としています。“変分”という言葉は、微分積分学での微分の変化率を指し、最適化問題における条件の変化率の最適化を目指しています。変分問題は、物理学、工学、経済学などの分野で頻繁に登場し、様々な問題に対処するために使用されます。
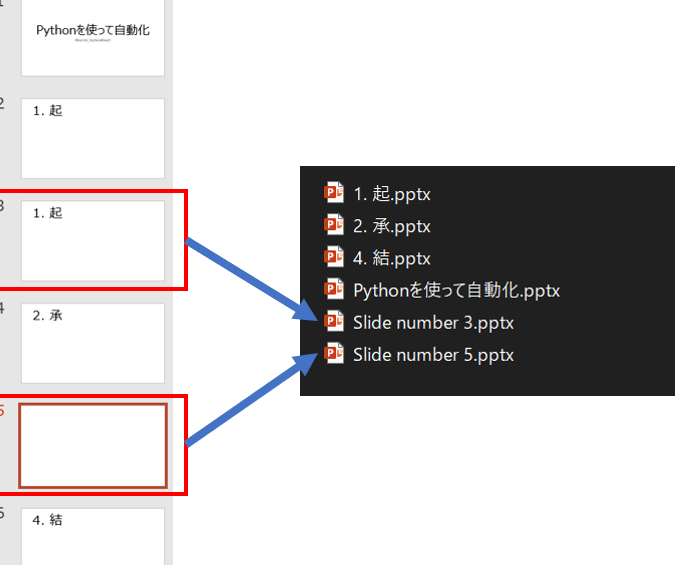
【Python】PowerPointのスライド分割&保存を自動化!Q2: Pythonで変分問題を解くための必要条件は何ですか?
Pythonで変分問題を解くための必要条件としては、主要に数学的な知識とプログラミングスキルが挙げられます。数学的な知識として、微分積分学、線形代数、最適化理論などに関する基礎知識が必要です。また、プログラミングスキルとしては、Pythonの基本的な文法、NumPy、SciPyなどのライブラリの使用方法、制御構文や関数の使用方法などが必要です。
Q3: 変分問題の計算例はどのようなものですか?
変分問題の計算例としては、物理学における運動エネルギーの最小化、経済学におけるコストの最小化、機械工学における構造の最適化などが挙げられます。これらの問題では、与えられた条件下での最小値や最大値を探索するために、変分問題を適用します。具体的には、Pythonを用いて、微分方程式や積分式を用いて計算を行い、最適な解を探索します。
Q4: 変分問題を学ぶことで何が得られますか?
変分問題を学ぶことで、最適化問題に対処するための数学的なツールを獲得できます。また、Pythonを用いて変分問題を解くことで、プログラミングスキルを向上させることができます。また、変分問題を学ぶことで、様々な分野での問題に対処するための視野を広げることができます。例えば、物理学、工学、経済学などでの問題に対処するための分析能力を高めることができます。
【Raspberry Pi入門】Minecraft Pi Editionの基本操作まとめ