【ゲーム理論入門】零和ゲーム、混合戦略、相関戦略を解説
ゲーム理論とは、数学的な手法を用いて人間の意思決定や戦略的な思考を分析する学問分野である。ゲーム理論入門として、本稿では零和ゲーム、混合戦略、相関戦略を中心に、ゲーム理論の基礎概念を紹介する。なぜ人間は特定の選択をし、どのように戦略を立てるのかを数学的に捉えることで、ゲーム理論はビジネスや政治、スポーツなど、多くの分野で応用されてきた。vangstionは、ゲーム理論を通じて、人間の意思決定をより深く理解し、新しい洞察を得ることを目指す。
【ゲーム理論の基礎】零和ゲーム、混合戦略、相関戦略を学ぼう
ゲーム理論は、数学を基にして、意思決定や戦略を分析するための理論です。この分野では、ゲームと呼ばれる状況下での意思決定や相互作用を捉えるために、様々な概念や戦略が提案されています。この記事では、ゲーム理論の入門として、零和ゲーム、混合戦略、相関戦略について解説します。
【零和ゲームとは】相手を倒すための戦略
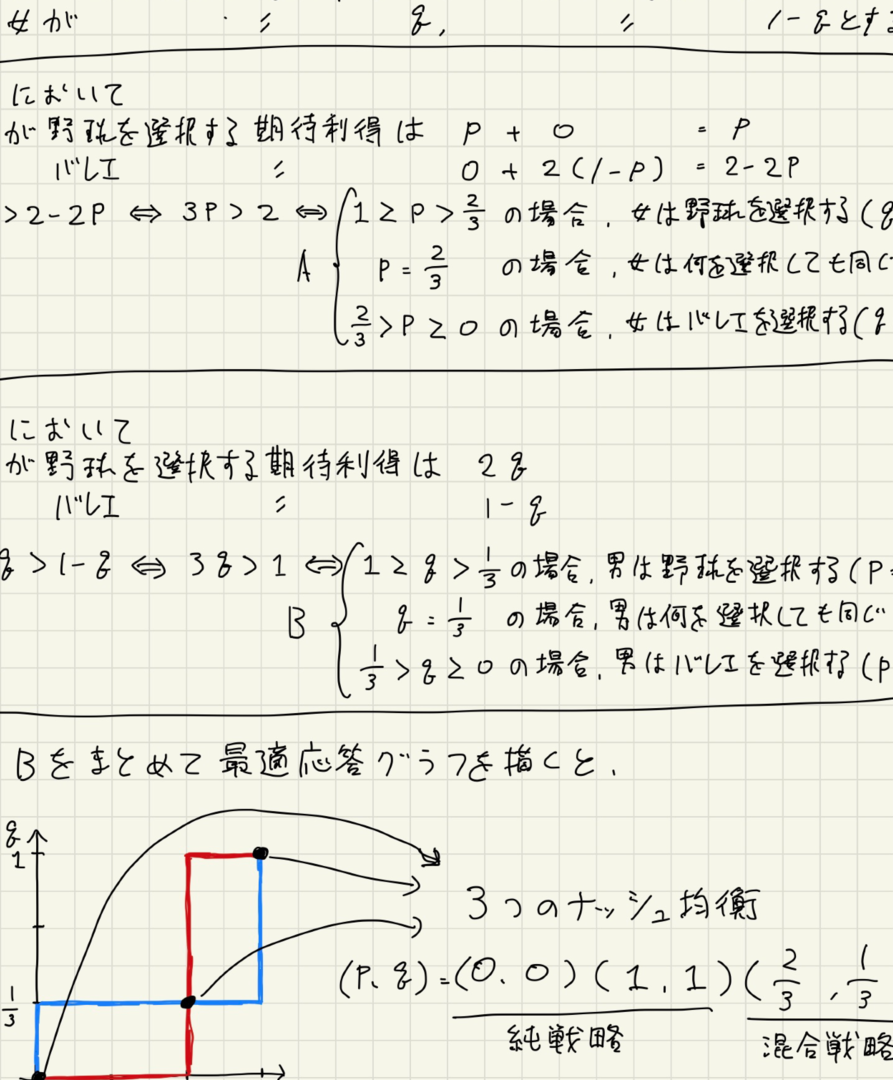
零和ゲームは、一人の勝利がもう一人の敗北を意味するゲームを指します。このゲームでは、双方の利益は反対方向にあり、片方の勝利は他方の敗北を意味します。零和ゲームでは、ナッシュ均衡という概念が重要です。ナッシュ均衡とは、自己の戦略を変更しても、結果が改善しない状態を指します。
【スプレッドシート】条件付き書式とGASでセルを色分け!【混合戦略とは】ランダムに行動する戦略
混合戦略は、ランダムに行動する戦略を指します。この戦略では、複数の戦略からランダムに選択することで、相手の予測を困難にします。混合戦略には、混合ナッシュ均衡という概念があります。混合ナッシュ均衡とは、混合戰略の状態で、自己の戦略を変更しても、結果が改善しない状態を指します。
【相関戦略とは】協力による利益の最大化
相関戦略は、協力によって利益を最大化する戦略を指します。この戦略では、相手との協力によって、双方の利益を最大化します。相関戦略には、囚人のジレンマという問題があります。囚人のジレンマとは、相互の利益が相反する場合、協力が崩壊する問題を指します。
【ゲーム理論の応用】ビジネスや政治での活用
ゲーム理論は、ビジネスや政治など、様々な分野での意思決定や戦略を分析するために応用されています。この理論を応用することで、最適な意思決定や戦略を立てることができます。
【ゲーム理論の歴史】(uriogeoryō no rekishi)
ゲーム理論の歴史は、20世紀初頭に始まります。 جون・フォン・ノイマンやオスカー・モルゲンシュターンらの研究によって、ゲーム理論は発展しました。
【プロジェクト管理】マイルストーン作成の6ステップ&注意点| ゲームの種類 | 説明 |
|---|---|
| 零和ゲーム | 一人の勝利がもう一人の敗北を意味するゲーム |
| 混合ゲーム | ランダムに行動するゲーム |
| 相関ゲーム | 協力によって利益を最大化するゲーム |
ゲーム理論の3要素は?

ゲーム理論の3要素は、戦略、payoff、 information です。
戦略
ゲーム理論における戦略とは、プレイヤーが採用する行動のルールのことです。
- ミックス戦略
- 純粋戦略
- 随伴戦略
これらの戦略を組み合わせることで、ゲームの勝敗を決定します。
【タスク管理】業務効率化!タスク管理を正確に行う4つのステップpayoff
payoffとは、ゲームの結果によってプレイヤーが得る報酬やペナルティのことです。
- 勝利報酬
- 敗北ペナルティ
- 引き分け報酬
payoffの設定によって、ゲームの性質が変わることがあります。
情報
情報とは、ゲームの進行中になどプレイヤーが持つ情報のことです。
- 完全情報
- 不完全情報
- 暗黙の了解
情報の有無によって、ゲームの戦略が変わることがあります。
【デザイン】基本原則!近接・整列・反復・対比を理解しようゲーム理論における混合戦略とは?
ゲーム理論における混合戦略とは、複数の純粋戦略の混合によって、均衡策を定める戦略である。ナッシュ均衡の概念に基づいて、ゲーム参加者が相手の行動を予測し、相手の期待値に対応することで、自分の利得を最大化する戦略を考える。
混合戦略の例
混合戦略の例として、カードゲームのポーカーを挙げることができる。ポーカーでは、プレイヤーはカードの強さに応じて、賭け金を設定する必要がある。この場合、プレイヤーがすべてのカードについて同一の戦略をとることは不可避的に敗北に繋がる。一方、混合戦略を取ることで、相手の予測を撹乱し、自分の利得を最大化することができる。
- 混合戦略によって、相手の予測を撹乱することができる。
- 自分の利得を最大化することができる。
- ゲームの不透明さを高めることができる。
混合戦略の特徴
混合戦略の特徴として、以下のような特徴が挙げられる。
- 予測不能:混合戦略を取ることで、相手の予測を撹乱することができる。
- 同時均衡:混合戦略は、複数の純粋戦略の混合であるため、同時に複数の均衡状態を実現することができる。
- 最適化:混合戦略は、ゲーム参加者の利得を最大化することを目指す。
混合戦略の問題点
混合戦略には、以下のような問題点も存在する。
- 計算コスト:混合戦略を計算するためには、高い計算コストがかかる。
- 情報の不足:ゲーム参加者の情報が不足している場合、混合戦略を設定することが困難になる。
- 対戦相手の念頭:ゲーム参加者の念頭を読むことができない場合、混合戦略の効果が減少する。
ゲーム理論における戦略とは?

ゲーム理論における戦略とは、ゲームにおいて、プレイヤーが目的達成のために選択する一連の行動のことを指します。ゲーム理論において、戦略は、プレイヤーの意思決定や、ゲームの結果に影響を与える要因として捉えられます。
戦略の分類
ゲーム理論における戦略は、純粋戦略と混合戦略に分類されます。
- 純粋戦略:プレイヤーが一つの行動を選択する戦略。
- 混合戦略:プレイヤーが複数の行動をランダムに選択する戦略。
- また、戦略の評価尺度として、支払い関数や最適応答も重要な概念です。
戦略の形成要因
ゲーム理論における戦略の形成要因として、ゲームの規則、プレイヤーの_preference_、情報のあり方などが挙げられます。
- ゲームの規則:ゲームの勝敗条件や、プレイヤーの行動の自由度など。
- プレイヤーの_preference_:プレイヤーの好みや価値観。
- 情報のあり方:ゲーム中での情報の開示や隠蔽など。
戦略の実際的な応用
ゲーム理論における戦略の実際的な応用として、経営戦略、政治戦略、軍事戦略などが挙げられます。
- 経営戦略:企業の経営estrategya。
- 政治戦略:政治的目的達成のための戦略。
- 軍事戦略:軍事的目的達成のための戦略。
パレート最適とはゲーム理論で何ですか?

パレート最適は、ゲーム理論において、複数の参加者による意思決定の問題において、各参加者の利得を最大化するために、妥協点を探索するための理論的手法です。パレート最適という言葉は、ヴィルフレド・パレートというフランスの経済学者にちなんで名づけられています。
パレート最適の定義
パレート最適は、複数の参加者が、各自の利得を最大化するために、妥協点を探索することを目的としています。この場合、各参加者の利得は、他の参加者の利得に影響を受けるため、複雑な意思決定の問題を生じます。パレート最適は、このような問題を解くために、数学的手法を用いて、妥協点を探索します。
- 複数の参加者による意思決定
- 各参加者の利得を最大化
- 妥協点の探索
パレート最適の特徴
パレート最適には、以下のような特徴があります。効率性という言葉が、パレート最適の特徴の一つです。これは、各参加者の利得を最大化するために、妥協点を探索するという意味合いです。また、パレート最適は、公平性という観点からも捉えることができます。これは、各参加者の利得を、公平に分配することを目的としています。
- 効率性
- 公平性
- 妥協点の探索
パレート最適の応用
パレート最適は、ゲーム理論や経済学のみならず、政策決定や国際関係にも応用されています。国際関係における、国家間の協力や対立は、パレート最適の概念を用いて分析することができます。また、政策決定における、複数の利益集団の調整も、パレート最適の概念を適用することができます。
- 国際関係
- 政策決定
- 利益調整
よくある質問
Q1: ゼロ和ゲームとは何か?
ゼロ和ゲームは、ゲーム理論における基本的な概念の一つです。ゼロ和ゲームとは、プレイヤーの勝敗が互いに反比例するゲームのことを指します。つまり、あるプレイヤーの勝利は、他のプレイヤーの敗北を意味し、vice versaです。このようなゲームでは、プレイヤーの合計得点はゼロになります。この概念は、経済学や政治学、マネジメント論など広範囲にわたって応用されています。
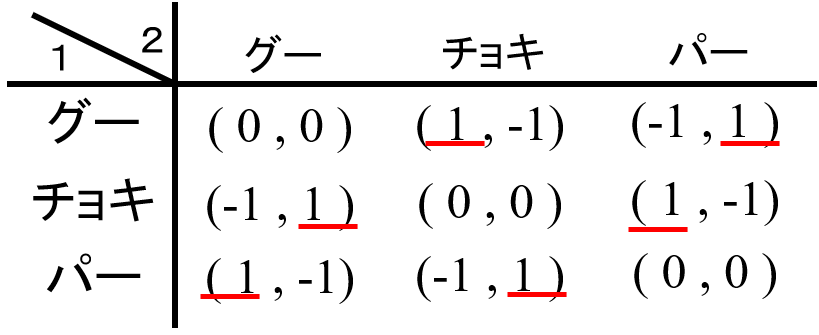
Q2: 混合戦略とは何か?
混合戦略は、ゲーム理論における戦略の一つです。混合戦略とは、複数の純粋戦略を一定の確率で選択する戦略のことを指します。つまり、プレイヤーは、複数の戦略を用意し、各戦略を選択する確率を設定します。この戦略を用いることで、プレイヤーは相手の予測を困難にし、より良い結果を得ることを目指します。混合戦略は、ゼロ和ゲームや非ゼロ和ゲームの両方で有効的に活用できます。
Q3: 相関戦略とは何か?
相関戦略は、ゲーム理論における戦略の一つです。相関戦略とは、プレイヤーが相手の戦略に相関して自分の戦略を決定する戦略のことを指します。つまり、プレイヤーは相手の戦略を予測し、自分の戦略を調整します。この戦略を用いることで、プレイヤーは相手との相互作用に応じて自分の戦略を最適化することができます。相関戦略は、ゼロ和ゲームや非ゼロ和ゲームの両方で有効的に活用できます。
Q4: ゲーム理論の応用はどこにあるのか?
ゲーム理論の応用は、非常に広範囲にわたります。経済学では、ゲーム理論は、市場の競争や寡占の分析に用いられます。また、政治学では、ゲーム理論は、国際関係や選挙戦略の分析に用いられます。さらに、マネジメント論では、ゲーム理論は、企業の戦略や意思決定の分析に用いられます。また、ゲーム理論は、コンピューターサイエンスや生物学などの分野でも応用されています。